Gravity is a curious thing. On an everyday level, almost all of us experience it in such a steady, unchanging way that it vanishes from our conscious attention. From time to time we notice change – the sudden acceleration of a lift in a tall building, or a ride in a theme park. A few people fly aircraft in such a way as to handle serious g-forces, and an even smaller handful have been in the microgravity of Earth’s orbit (or a very specific aircraft trajectory intended to mimic conditions in space). But for most of us, most of the time, it is just there as a constant part of our environment.

In terms of physics, gravity is the odd one out of the standard four forces of nature (the others being electromagnetism, plus the weak and strong nuclear forces). It is odd for a couple of reasons – first, it is immensely weaker than the others, but secondly, it is always an attractive force rather than sometimes attracting and sometimes repelling… so far as we known in 2019. There has been a recent report of a Hungarian team discovering a fifth force, but this has not been confirmed by other teams yet, and in any case will not change the gist of this blog post. The forces other than gravity tend to cancel out over any great distance, and only really affect things on very short distances. But gravity, despite its comparative weakness, really does shape the way the universe looks and behaves.

Gravity in films usually gets treated in very cavalier ways. The most striking example of this is the 2013 film Gravity, which was built on an interesting premise but often failed at the science. In one especially memorable moment, George Cluny’s character tells Sandra Bullock’s, that in order to get over to the Chinese orbital station, she just has to keep it in the centre of the viewport and keep firing the engines. In terms of orbital mechanics, it would be hard to arrive at a less likely option for reaching her target. It would work for fairground dodgem cars, or for boats on a stretch of open water: it would even work pretty well for two aircraft in flight. But two bodies in space, in orbit around a central body behave in ways that can be counter-intuitive, and the whole aim-and-accelerate idea is pretty much doomed to failure.

It’s an odd thing that gravity, even in Newton’s classical world where relativity and quantum mechanics play no part, is such a hard system to solve. If the entire universe consisted of just two objects, then their future motion could be exactly predicted for as far ahead as you please. But with more than two objects – starting with the so-called three-body problem – there is no general exact solution. A few special cases can be solved to a good-enough accuracy, and there are some very hypnotic numerical simulations of the resulting tracks, but the general case remains unsolved. Even a partial answer is better than none at all, however, and one of the most strikingly useful examples of three-body interactions is the so-called gravity assist manoeuvre (also called a slingshot) in which a space probe is given a substantial acceleration by means of a close approach to a convenient planet.

From a story-telling perspective, three-body problem solutions are very handy! Gravity assists are a great way to make a journey achievable, which otherwise would take too long to complete. And some other very convenient solutions are the so-called Lagrange points – “fixed” places holding a particular relationship with a planet in its orbit. A small body – a spaceship, or a small asteroid – which is placed into one of those points will remain there in a stable configuration, whereas at other nearby locations, the relative orbits will diverge rather than converge. Most planets in the solar system have accumulated a little cluster of small natural bodies at the points L4 and L5 – these are generically called Trojan satellites, following a convention established for the moons of Jupiter. Even Earth has at least one Trojan satellite, whereas Jupiter has over 7000 of them. The Lagrange points provide a very convenient “resting-place”, where an author can locate an artificial satellite without needing to exert any station-keeping energy.

These represent gravitational solutions which are useful, in a sort-of utilitarian manner. However, the long-distance and always-attractive qualities of gravity also give rise to exciting and rather surprising patterns of motion. These represent resonant patterns which can often stabilise a system, making it longer-lasting than might be expected. For example, the orbit of Pluto occasionally crosses over that of Neptune. One’s first thought is that at some point they would collide, or at least get close enough to seriously interfere with each other’s orbit. In fact their orbits are in a 2:3 resonant pattern with each other – for every three orbits of Neptune, Pluto makes two. This, together with some other resonances in their orbits, means that the two planets never in fact approach one another very closely at all. They remain stable. Similar stable patterns can be seen in the orbits of bodies outside Pluto, in the Kuiper Belt. Resonance can destabilise systems as well – there are gaps in the asteroid belt caused by resonances with Jupiter, and gaps in Saturn’s rings caused by one or other of the moons. But I want to finish this section with a stabilising resonance which turns out to be particularly appealing – Naiad and Thalassa, two of the moons of Neptune, are constantly engaged in an orbital dance to avoid each other. The ratio is particularly complicated in this case: for every 69 orbits of Thalassa, Naiad orbits 73 times.

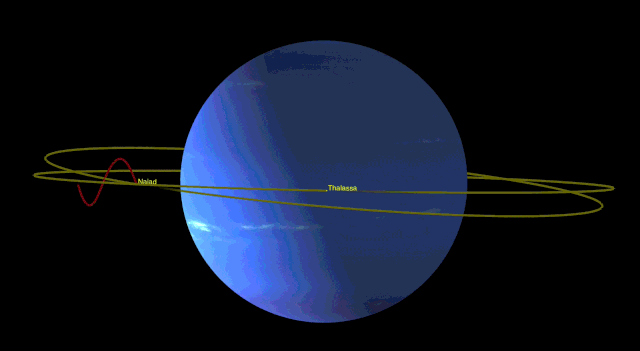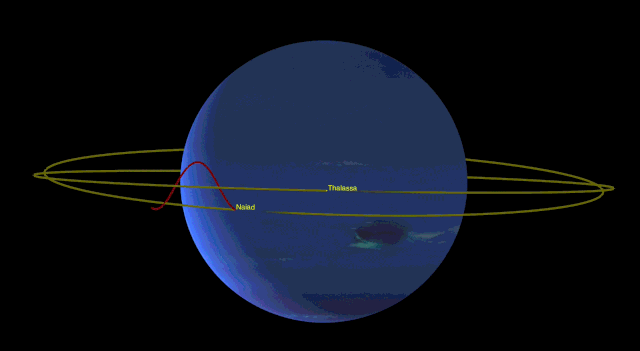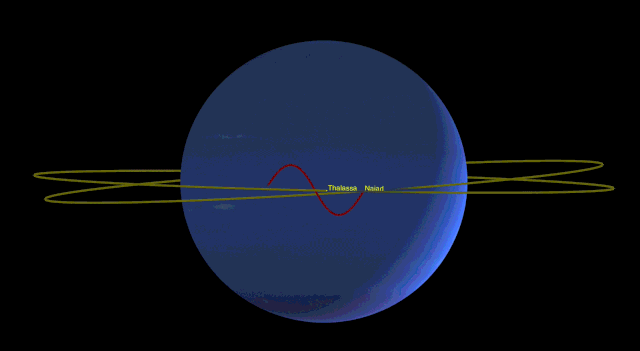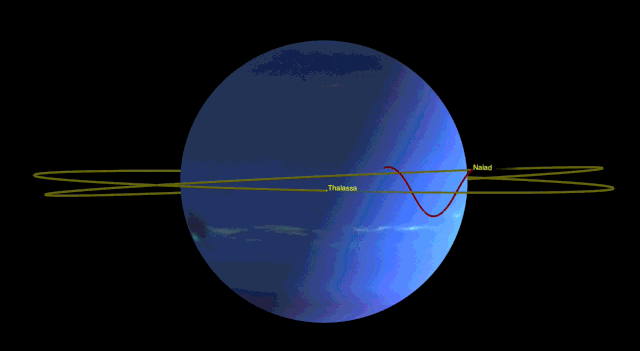
So gravity is a complicated thing, and at least when you’re in orbit, can’t be solved by simply aiming-and-shooting. But it does give rise to some exciting possibilities for stories, and some fascinating choreography amongst planets, moons, and asteroids. Of which, more another time.